ML Optimization Surrogates
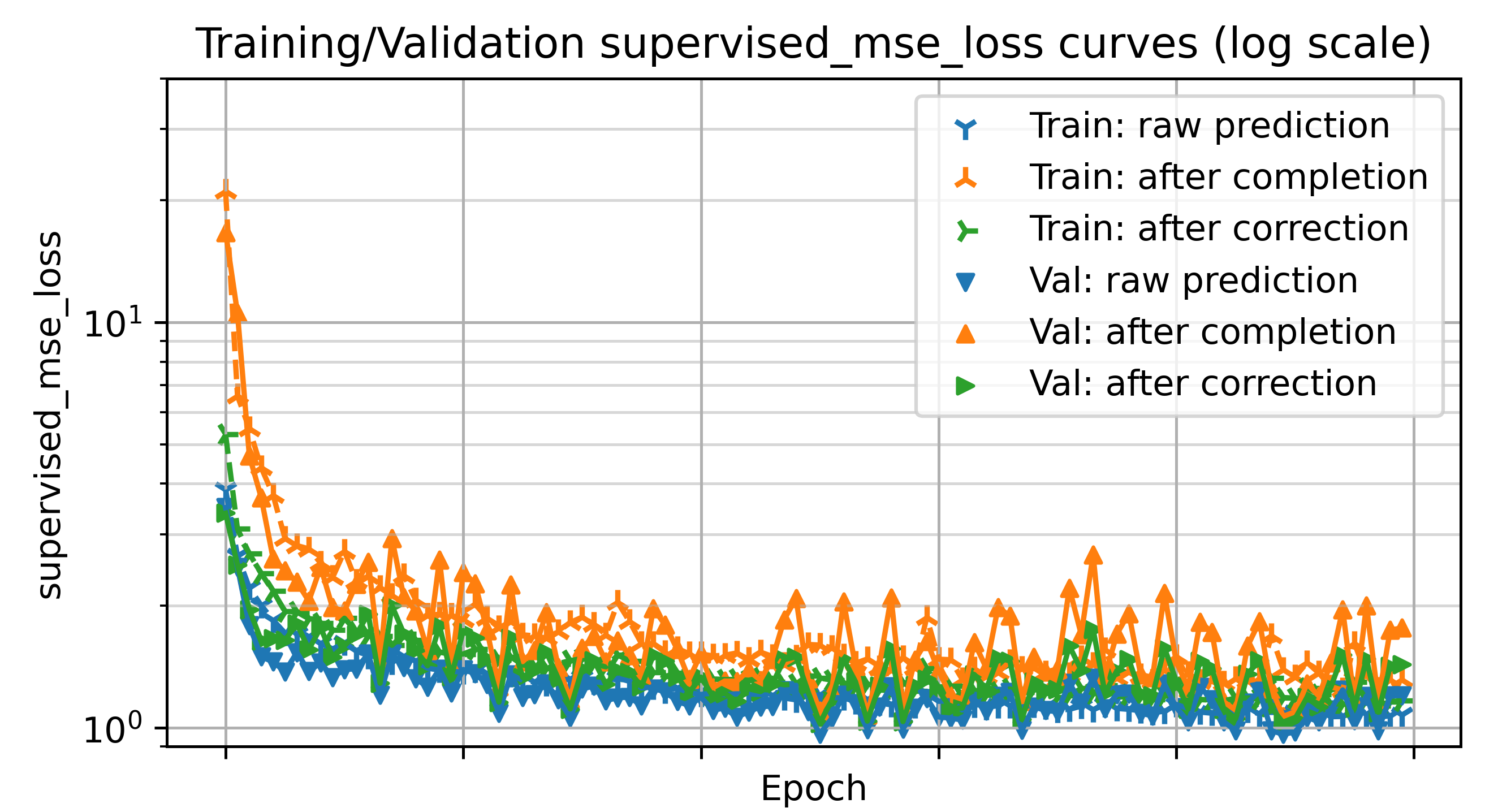
The above learning curve (not finalized, should not be cited, etc.) shows a very early version of our DC3-based optimization surrogate learning to solve mixed-integer linear programs. The blue curves depict the initial output of the neural network, which somewhat closely matches the true solution but with substantial equality constraint violation (not shown). The completion procedure in orange eliminates equality constraint violations at the cost of decreased solution accuracy, then the correction procedure (green) brings the solution back closer to the true value and reduces inequality constraint violation (not shown) while maintaining equality constraint satisfaction.
Quick links: open the above image in a new tab. More resources hopefully coming soon!
At their core, operational power simulations that help us answer important questions about how to build a sustainable, resilient power grid are based on sequences of interrelated mathematical optimization problems. Some types of problems, such as unit commitment, which determines how to turn on and off electrical generators to meet a certain amount of demand for electricity while minimizing cost, are often best formulated as mixed-integer linear programs (MILPs). The ‘mixed-integer’ part in particular makes these tricky to solve quickly, creating a bottleneck that limits the number of scenarios a grid researcher can simulate to more robustly answer a particular question. So my PI José Daniel Lara and I proposed and received a $45,000 internal NREL grant to study how machine learning surrogates might be harnessed to solve these sorts of problems faster than traditional solvers at the cost of a small drop in accuracy.
As in my other main contemporaneous ML project, a raw neural network is likely not up to the challenge. We began our investigation by studying various algorithms that augment a neural network with hand-designed layers, such as OptNet, Google DeepMind’s CANOS, DC3, and FSNet, creating working mini-replications of each. We settled on DC3, which uses a neural network to generate raw predictions for some of the variables in the optimization problem, then solves the equality constraints for the rest of the variables (“completion”), then performs some unconstrained optimization to satisfy the inequality constraints (“correction”). Consulting DC3’s lead author Priya Donti and her student Lara Booth, we set about adapting DC3 for use with these real-world MILPs.
Inspired by CANOS, our method transforms an optimization problem into a bipartite graph representing variables and constraints as nodes. We then use a heterogeneous graph transformer network to process this into a set of raw predictions to feed into the completion and correction steps of DC3. We’re still working, but so far we’ve been excited by this novel neural network architecture’s ability to make use of the structure of the optimization problem while remaining applicable to a very wide range of MILPs that come up in power grid simulation.
Another focus of our work has been integrating this surrogate with Sienna, the open-sourve power grid simulation platform we’ve developed at NREL. Work is ongoing here as well, but we have a prototype workflow where the user can specify the surrogate just like how they would specify a traditional solver, the surrogate will try the problem and defer to a traditional solver if it is not able to achieve sufficient accuracy, and the problem will be added to a dataset for in-the-loop surrogate training. We’re also considering other workflows, including pre-training surrogates for certain large, oft-reused power systems and an even broader foundation model approach. Stay tuned for updates!